Voronoi Integration
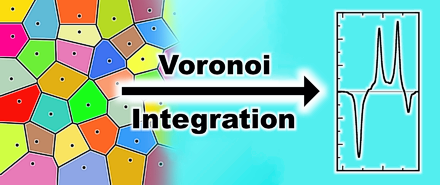
In 2015, my colleague Martin Thomas and me have developed and published the Voronoi integration technique. This method applies a periodic radical Voronoi tessellation in three-dimensional space to the atom positions, and subsequently integrates the total electron density within each molecule's Voronoi cell to obtain molecular electromagnetic moments such as the electric dipole vector or the electric quadrupole tensor. These quantities are required to compute vibrational spectra from ab initio molecular dynamics simulations, as we have demonstrated for infrared, Raman, VCD, ROA, and resonance Raman spectra.
"Voronoi Dipole Moments for the Simulation of Bulk Phase Vibrational Spectra",
Phys. Chem. Chem. Phys. 2015, 17, 3207–3213. DOI 10.1039/C4CP05272B
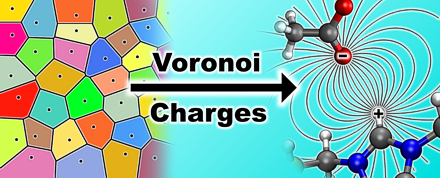
Based on the radical Voronoi tessellation, we have developed a method for computing optimized atomic partial charges (“Voronoi charges”) from AIMD. The radii are optimized on-the-fly to minimize the molecular and atomic charge fluctuations, so that the approach does not possess any empirical parameters and yields a rigorous definition of atomic charges in the condensed phase.
"Optimized Atomic Partial Charges and Radii Defined by Radical Voronoi Tessellation of Bulk Phase Simulations",
Molecules 2021, 26 (7), 1875. DOI 10.3390/molecules26071875
The Voronoi tessellation is based on the Voro++ library which was written by Chris Rycroft.
— Availability —
Since the article was published in 2015, the Voronoi integration technique is implemented in the TRAVIS program package. TRAVIS can read Cube files with the total electron density of the system, and subsequently perform the Voronoi integration to obtain molecular electromagnetic moments and compute vibrational spectra. There is also a step-by-step tutorial available which shows how to compute bulk phase vibrational spectra with TRAVIS and CP2k.
During my guest visit at the University of Zurich, I have implemented the Voronoi integration method directly into the CP2k program package. Starting from CP2k release 8.1 (December 2020), it is possible to directly compute the electromagnetic moments during a CP2k simulation without having to output the total electron density in every step. An updated version of the tutorial will follow soon.
See the &DFT/&PRINT/&VORONOI manual section.
Note: If you compile CP2k 8.1 or newer via the Toolchain script, these features will automatically be included by default, and the library will automatically be downloaded and compiled in the process. If you prefer not to use the Toolchain, you need to download and compile the libvori source code from here.
— Advantages over Wannier Localization —
To show the power of our new method, we will compare it to the standard approach for computing molecular dipole moments in condensed phase systems, which is the Wannier localization, which leads to maximally localized Wannier functions (MLWFs):
- Our implementation of the Voronoi integration (as found in TRAVIS and CP2k) is very fast. For a bulk phase system with 1000 atoms, the Voronoi integration only takes around 2 seconds on a single CPU core, while the Wannier localization takes around 30 seconds on 16 cores (using the “crazy angle” algorithm in CP2k; with Jacobi diagonalization, it even takes much longer).
- The Wannier localization is an iterative method, and is not guaranteed to converge. It can happen that a large number of iterations is required, or that no convegred result at all can be obtained. The Voronoi integration is non-iterative, and its runtime is predictable (and almost constant for identical atom count and grid resolution).
- The Wannier localization has severe problems with aromatic systems, because it localizes the aromatic structure to a single bond/double bond pattern, which can flip from time to time during the simulation. This introduces artificial peaks into the infrared spectrum, and makes the calculation of Raman spectra all but impossible, as we discuss in our article. The Voronoi integration, on the other hand, works flawlessly for aromatic systems.
- The Voronoi integration only requires the total electron density on a Cartesian grid as input, and is therefore very easy to attach to all different kinds of electron structure methods and quantum chemistry software. Most quantum chemistry packages can output the total electron density as a CUBE file, so the Voronoi integration can be performed without any changes to the software.
- In contrast to the Wannier localization, which can only give electric dipole moments, the Voronoi integration also yields higher electric multipole moments, such as the quadrupole tensor, which is e.g. required for computing ROA spectra.